| cgg_draft_19_1_2015.pdf |
Abstract: This paper introduces the concept of a Forecast Combination Equilibrium to model boundedly rational agents who combine a menu of different forecasts using insights from the forecasting literature to mimic the behavior of actual forecasters. The equilibrium concept is consistent with rational expectations under certain conditions, while also permitting multiple, distinct, self-fulfilling equilibria, many of which are stable under least squares learning. The equilibrium concept is applied to a simple Lucas-type monetary model where agents engage in constant gain learning. The combination of multiple equilibria and learning is sufficient to replicate some key features of inflation data, such as time-varying volatility and periodic bouts of high inflation or deflation in a model that experiences only i.i.d. random shocks.
Highlights:
Application: A Lucas-type Monetary Model: (For more detail see pdf of the paper above)
Consider a simple model consisting of an aggregated demand, aggregate supply, and monetary policy rule:
Highlights:
- The paper introduces the Forecast Combination Equilibrium concept.
- The concept permits multiple, E-stable equilibria.
- The existence of multiple equilibria depends both on the policy parameters of the model and the menu of forecast rules considered.
- The equilibrium concept, when combined constant gain learning of the parameters and optimal weights, generates time-varying volatility and endogenous breaks in the trend of the endogenous variables.
Application: A Lucas-type Monetary Model: (For more detail see pdf of the paper above)
Consider a simple model consisting of an aggregated demand, aggregate supply, and monetary policy rule:
The three equations imply that the inflation process for the economy follows an expectational Phillips curve:
I assume that instead of rational expectation the agents that inhabit this economy have model uncertainty. The agents posit two different misspecified rules to form forecasts:
The agents use model combination in order to form expectations
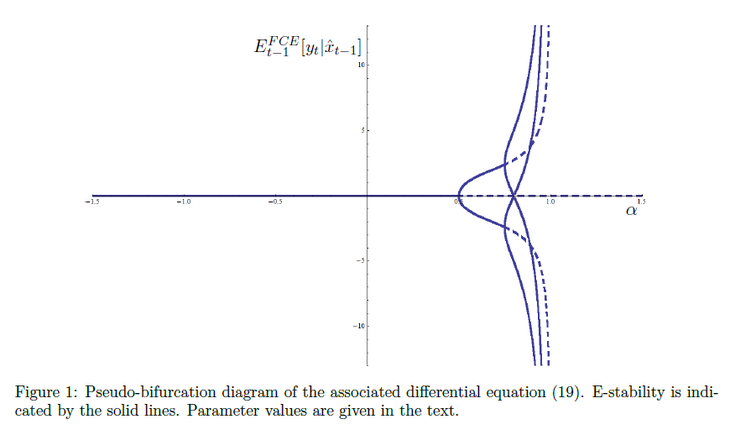
Finally, the agents are assumed to pick weights to minimize the expected squared forecast error of the combined forecast. This assumption results in multiple equilibria in the model. The multiple equilibria result is best demonstrated using a pseudo-bifurcation diagram, which plots the equilibrium combined forecast for a fixed realization of shocks.
The stability of the equilibria if agents engage in least squares learning of the parameters is denoted by the solid and dashed lines. Stable equilibria correspond to the solid lines. The stability and number of the equilibria also depend on the policy parameters of the model. If the response to the exogenous shock in the monetary policy rule is varied, the following equilibrium and stability results obtain: (See paper for parameter values.)
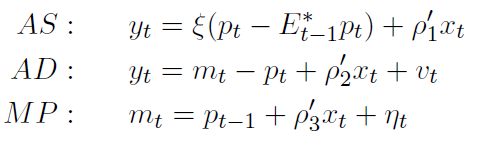
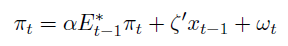
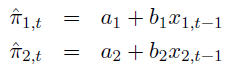
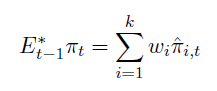

 RSS Feed
RSS Feed
